 PDF version of this document
PDF version of this document
Abstract. The need to establish correspondence across groups of images has for long been recognised. This problem is referred to as non-rigid registration. To enable comparative analysis of images depicting a similar object, analogous object structures must be identified and a practical way of doing so is by aligning these structures. The alignment is achieved by treating each image as a deformable object and transforming it to match another. One image is said to match another when it appears similar, i.e. objects within it overlap. A framework for a registration scheme comprises a measure of similarity (the objective function), a method of applying warps and an optimisation regime. Similarity measures assign an evaluative score to a collection of images that are subjected to transformations. That score reflects how good the alignment is and when it can no longer improve, convergence (i.e. registration) is assumed.
There is no agreement in the literature on what to consider a powerful family of transformations. It is also unclear what correctly defines similarity and which images should be compared when measuring that similarity. Popular methods are based on heuristics and results are difficult to validate. Our work addresses these issues, not by finding good registration schemes empirically, but by providing a well-founded approach to the problem. Since registration is known to reduce variation within groups of images, a model which represents these images will be accordingly affected. By looking at a model, we can derive similarity across the entire set, without the need for a reference. In a sense, the model is used here as a global similarity measure. Moreover, when models are used in the process of registration, statistical models are created, allowing variability in the dataset to be broken down into meaningful 'components' - the principal modes of model variation, which highlight attributes of interest. This functionality can aid identification of pathology symptoms in an autonomous manner. By registering raw sets of images of different groups, models can be built to find where greater variability lies.
The objective function presented in this work obtains similarity
indirectly. It does so by calculating the complexity of a combined
model of shape and intensity, namely by looking at the covariance
matrix of that model. To efficiently evaluate model complexity, we
obtained
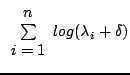 where
where
![]() are the
are the ![]() Eigen-values of the covariance
matrix whose magnitudes are the greatest. This approximates
Eigen-values of the covariance
matrix whose magnitudes are the greatest. This approximates
![\includegraphics[%
scale=0.16]{Graphics/test_on_target_7-4.eps}](img6.png)
![\includegraphics[%
scale=0.16]{Graphics/msd_gen_5_5-2.eps}](img7.png)
To demonstrate the advantages gained by the model-based approach, we experimented with one dimensional synthetic data where the correct solution is known. Generated data depicted a bump, a half-ellipse, which varied in height, width and position (see Figure 1). The sets were stochastically generated with significant variability that makes the problem challenging. We define a solution to be good when we observe proper alignment of the bumps and a resulting registered set that is distinct from any of the original images. At the same time, we are continuously delivered statistical models (as shown in Figure 3) of variable bumps. A combined model is derived from the shape model and the intensity model. Well-founded ways exist to visualise and evaluate them and it can be seen that the combined model is refined in the process, even after as little as 200 iterations.
After only a few minutes, good alignment amongst all bumps was obtained. Sets comprising dozens of bumps could be successfully handled by the algorithm and a statistical model of their appearance emerged as a by-product of registration. When compared with the known correct solution, the quality of registration was high. It also successfully surpassed naïve implementations of some conventional algorithms.
![\includegraphics[%
scale=0.16]{Graphics/align.ps}](img8.png)
![\includegraphics[%
scale=0.16]{Graphics/10000_-_second_attempt-2.eps}](img9.png)
As well as a basic model-based objective function, we investigated
the use of subsets to speed up the process. Subsets are chosen stochastically
every 100 iterations, thereby the problem is simplified and the algorithm
becomes more effective in dealing with large sets. It is worth adding
that choice of warps was random at all stages so no data-bias or
a-priori knowledge was involved.
![\includegraphics[%
scale=0.22]{Graphics/comb_start.eps}](img10.png)
![\includegraphics[%
scale=0.22]{Graphics/shape_start.eps}](img11.png)
![\includegraphics[%
scale=0.22]{Graphics/int_start.eps}](img12.png)
![\includegraphics[%
scale=0.2]{Graphics/comb_end.eps}](img13.png)
![\includegraphics[%
width=0.20\textheight,
height=1in]{Graphics/shape_end.eps}](img14.png)
![\includegraphics[%
scale=0.2]{Graphics/int_end.eps}](img15.png)
The results we have seen thus far suggest that our approach works properly while addressing common difficulties. It can handle large sets and provide a solution that does not depend on any arbitrary selection of images. Future work will apply this approach in a real-world problem by treating 2-D images and 3-D volumes of the human brain.