Why Evaluate?
Because certain methods neglect available information
Non-Rigid Registration
- Align images using
- spatial transformations
- similarity measures
Non-Rigid Registration
- Align images using
- spatial transformations
- similarity measures
Statistical Models
- Take a data set
- Find correspondences in set
- Learn how correspondences vary
Statistical Models
- Take a data set
- Find correspondences in set
- Learn how correspondences vary
Statistical Models
- Take a data set
- Find correspondences in set
- Learn how correspondences vary
Finding Correspondences
- Need for an automatic approach
- Difficulties in 3-D
- Non-rigid registration to align data
- Produce deformation fields/grid
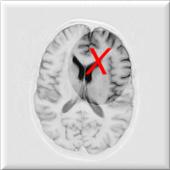
Finding Correspondences
- Need for an automatic approach
- Difficulties in 3-D
|
Where is a corresponding point in the volume? Picture from Johan Montagnat, INRIA |
Finding Correspondences
- Need for an automatic approach
- Difficulties in 3-D
- Non-rigid registration to align data
- Produce deformation fields/grid
Finding Correspondences
- Need for an automatic approach
- Difficulties in 3-D
- Non-rigid registration to align data
- Produce deformation fields/grid
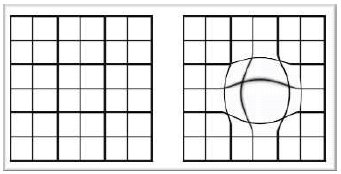
Finding Correspondences - ctd.
- Grids of deformation encapsulate variation
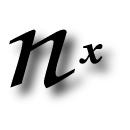
- Perform statistical analysis on grids
- Use model of variation for synthesis
Finding Correspondences - ctd.
- Grids of deformation encapsulate variation
- Perform statistical analysis on grids
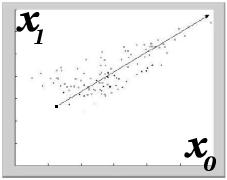
- Use model of variation for synthesis
Finding Correspondences - ctd.
- Grids of deformation encapsulate variation
- Perform statistical analysis on grids
- Use model of variation for synthesis
Model Construction
|
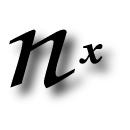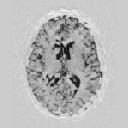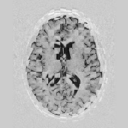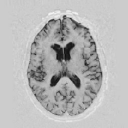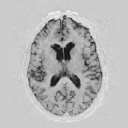
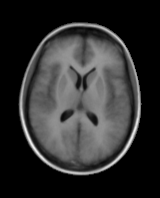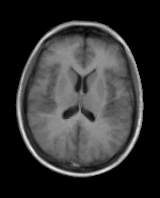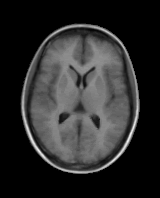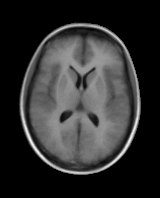 First variation mode 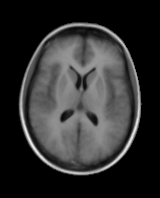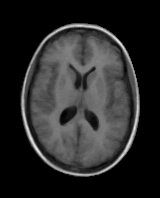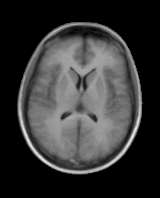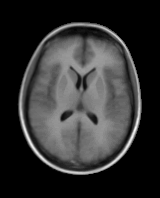 Second variation mode |
Degradation of Registration
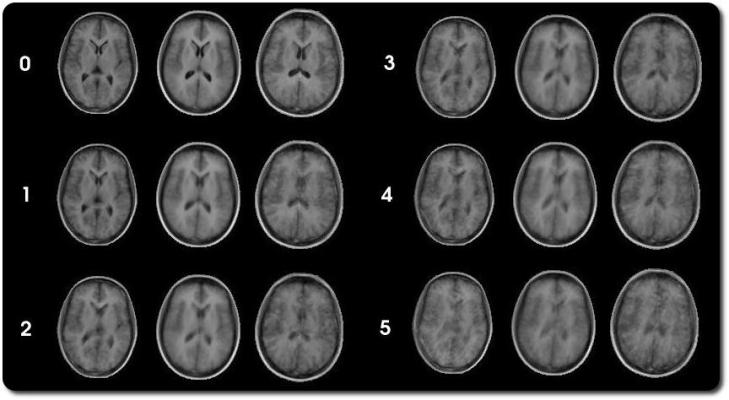
0 to 5 CPS warps perturbing the correct solution.
Shown is the first mode of the model, ±2.5 SD
Evaluation Method - Models
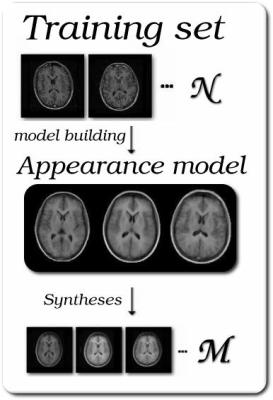
Model of the registered images and synthesis from the model
Evaluation Method - Abstraction
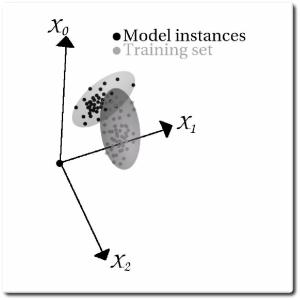
A hyperspace representation where 'clouds' of images overlap
Evaluation Method - Derivations
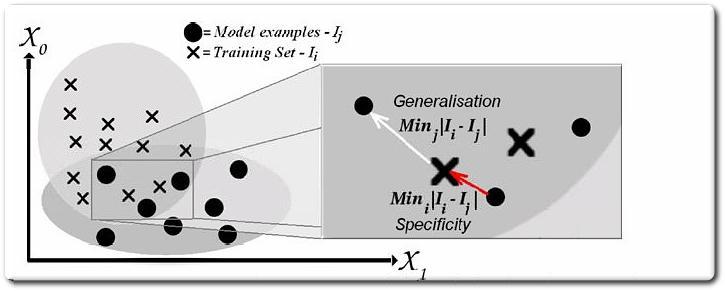
Calculating Specificity and Generalisation ability
Measuring Distance
- Distance naturally assumed Euclidean
- Shuffle distance performs better
Measuring Distance - Shuffle Distance
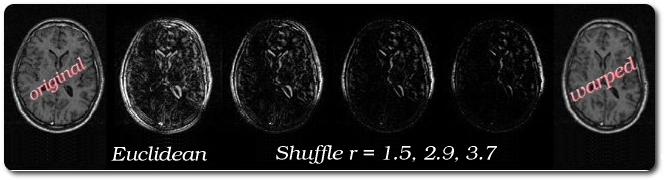
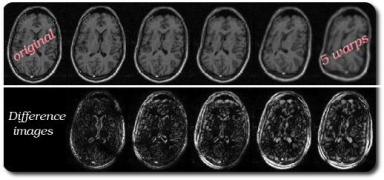
Validation of the Method
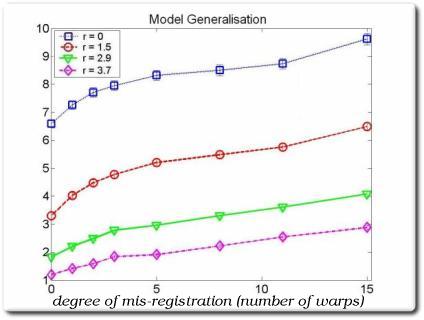
As correspondences degrade, so does Generalisability (low values are good)
Validation of the Method
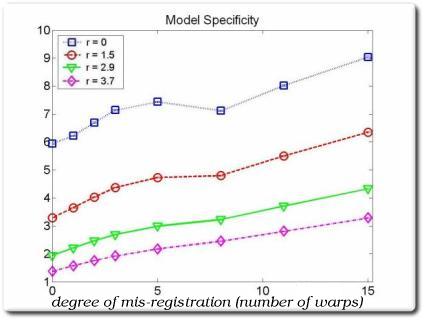
As correspondences degrade, so does Specificity
Validation of the Method
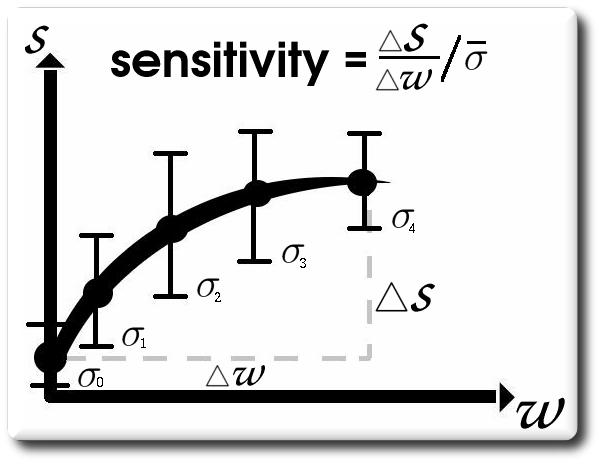
Investigate measures most sensitive to change
Validation of the Method
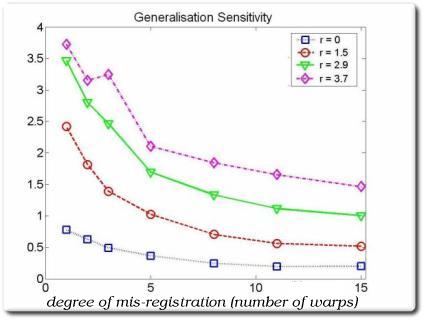
Shuffle distances covering a large region are sensitive to differences
Validation of the Method
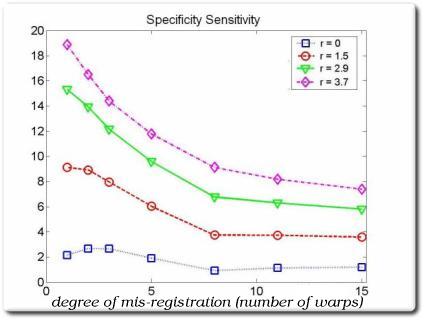
The choice of shuffle distance radius becomes an efficiency vs. performance trade-off
Evaluation of Registration
- Registration builds models automatically
- Model from group-wise registration presented below
- The evaluation requires no ground truth
Registration Algorithms - Comparison
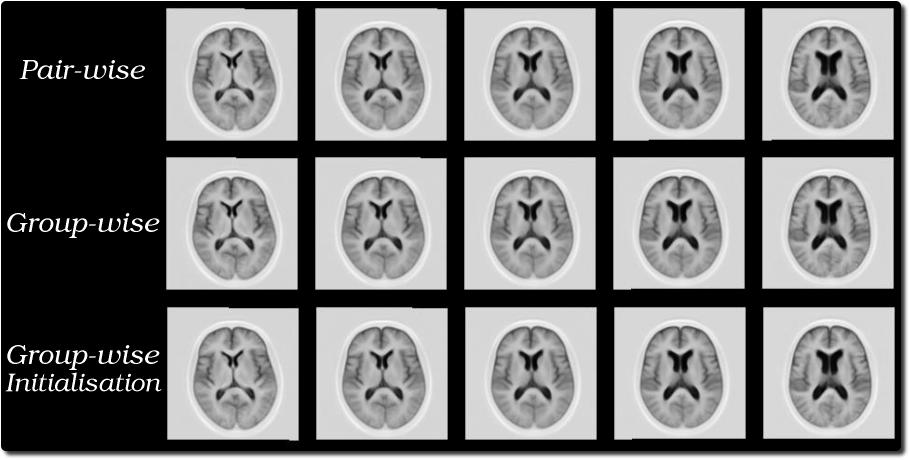
Group-wise methods surpass pair-wise regardless of the expressiveness of the model used
Visual Comparison
